

99클럽 코테 스터디 1일차 TIL - 백준 1929번 : 소수 구하기백준2025. 3. 31. 18:59
Table of Contents
항해99 클럽 코테 스터디 TIL - 자바 미들러 (3/30(월) ~ 4/28(월)) 시작!

https://www.acmicpc.net/problem/1929
✅ 문제

📌 접근방법
일반적인 소수 판별법으로 소수는 자기자신과 1만을 약수로 가지는 수이다.
n미만의 숫자 중에서 나머지 연산을 했을 때 0이 되면 약수를 가져서 소수가 아니다.
public class Algorithm {
static boolean isPrime(int n){ // 시간복잡도 O(N)
if(n<2){
return false; // 1은 소수가 아니기에 false
}else{
for(int i = 2; i < n; i++){
if(n % i == 0) return false; // 나머지연산을 했을 때 0이 나오면 소수가 아니므로 false
}
return true; // 위의 case
}
}
public static void main(String[] args)throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(br.readLine()); // 소수인지 판별할 숫자 input
System.out.println( (isPrime(N) == true) ? "소수입니다" : "소수가 아닙니다.");
}
}위 코드의 시간복잡도는 O(N)이며, N개의 수를 판별하면 O(N^2)이 된다.
시간이 상당히 오래걸리므로 에라토스테네스의 체로 접근했다.
에라토스테네스의 체는 많은 수의 소수판별을 할 때 유용하다.
이 알고리즘의 원리는 해당 숫자가 소수라면, 해당 숫자의 배수들은 모두 해당 숫자를 약수로 가지고 있으므로 소수가 되지 못한다.
- 먼저 지워지지 않는 가장 작은 수를 찾는다 -> 보통 2부터 시작한다.
- 해당 숫자는 소수이다.
- 해당 숫자의 배수들을 모두 지운다.
예시를 들어 설명하면 N이 100일 때 1~100 사이의 소수를 구해본다.
1은 예외이므로 제외하고 시작한다.
먼저, 지워지지 않는 가장 작은 수는 2이고, 2의 배수들은 소수가 아니므로 다 삭제한다.
(검은 글자는 소수거나 지워지지 않은 수, 회색 글자는 지워진 수)

그 다음 지워지지 않는 가장 작은 수는 3이고, 3의 배수들을 다 삭제한다.
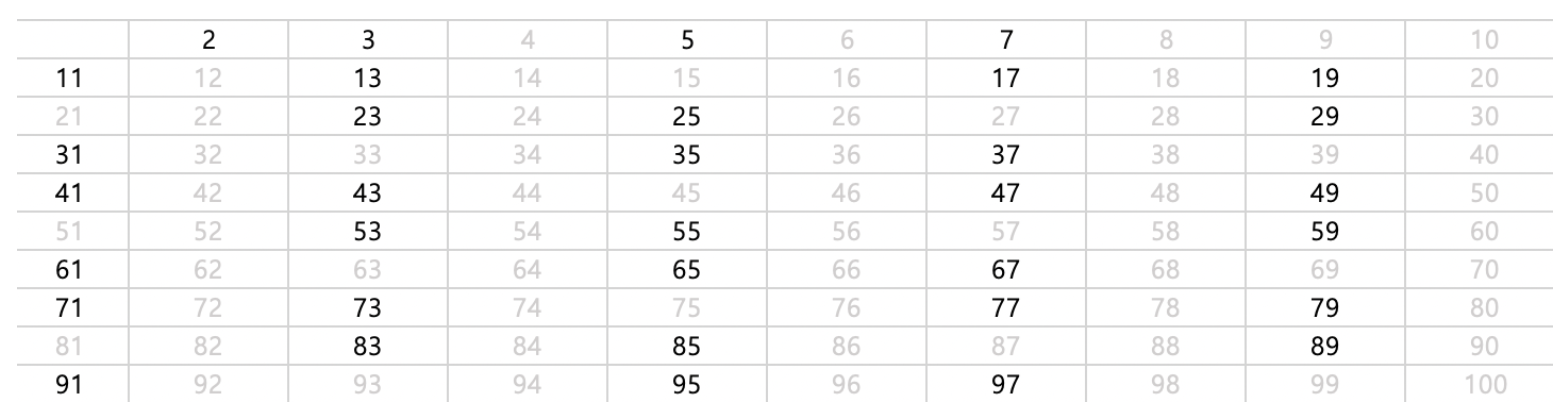
그 다음 지워지지 않는 가장 작은 수는 5이고, 5의 배수들을 다 삭제한다.
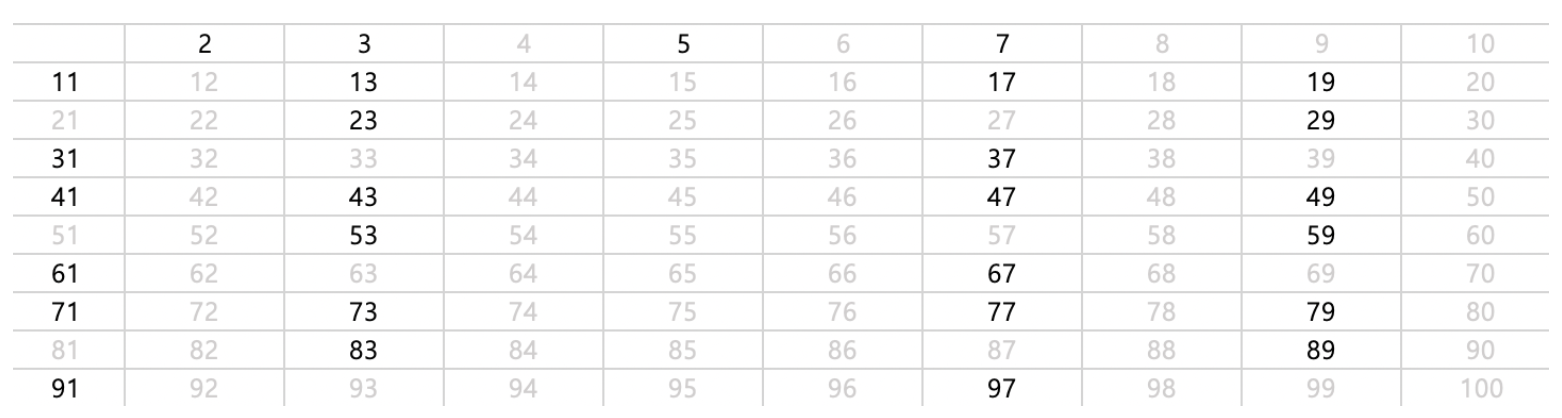
이러한 방식으로 하면 아래와 같이 소수들을 구할 수 있다.
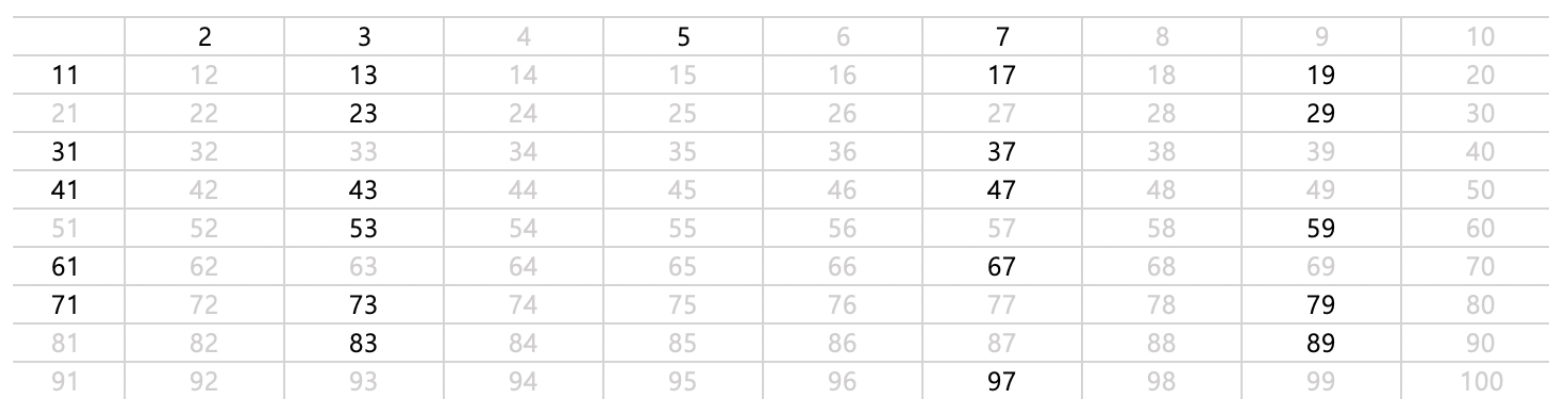
import java.io.*;
public class Algorithm {
static boolean[] isPrime;
static void isPrime_check(int n){
isPrime = new boolean[n+1]; // N번째의 수 까지 받기위해 N+1까지 동적할당
for(int i = 0; i < isPrime.length; i++){
isPrime[i] = true; // boolean배열의 default값은 false이므로 true로 바꿔주기
}
isPrime[0] = isPrime[1] = false; // 0과 1은 소수가 아니니깐 false
for(int i = 2; i <= Math.sqrt(n); i++){ // 2부터 n의 제곱근까지의 모든 수를 확인
if(isPrime[i]){ // 해당수가 소수라면, 해당수를 제외한 배수들을 모두 false 처리하기
for(int j = i*i; j<= n; j += i){//그 이하의 수는 모두 검사했으므로 i*i부터 시작
isPrime[j] = false;
}
}
}
}
public static void main(String[] args)throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(br.readLine()); // 소수인지 판별할 숫자 input
isPrime_check(N);
}
}위의 시간 복잡도는 O(Nlog(logN))이다.
🔑 풀이
에라토스테네스의 체 알고리즘을 활용하여 문제 풀이에 적용했다.
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
// 항해 코딩테스트 스터디 Day1 - 자바/미들러
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int M = Integer.parseInt(st.nextToken());
int N = Integer.parseInt(st.nextToken());
boolean[] isPrime = isPrime_check(N);
for (int i = M; i <= N; i++) {
if (isPrime[i]) {
System.out.println(i); // 소수인 경우, 출력
}
}
}
public static boolean[] isPrime_check(int n) {
boolean[] isPrime = new boolean[n + 1];
for (int i = 0; i < isPrime.length; i++) {
isPrime[i] = true; // 모든 수를 소수로 가정
}
isPrime[0] = false; // 0은 소수가 아님
isPrime[1] = false; // 1은 소수가 아님
// 에라토스테네스의 체 알고리즘
for (int i = 2; i <= Math.sqrt(n); i++) {
if (isPrime[i]) { // i가 소수인 경우
for (int j = i * i; j <= n; j += i) {
isPrime[j] = false; // i의 배수들은 소수가 아님
}
}
}
return isPrime;
}
}
실행 코드 (백준 페이지)
'백준' 카테고리의 다른 글
| 99클럽 코테 스터디 5일차 TIL - 백준 2559번 : 수열 (0) | 2025.04.04 |
|---|---|
| [누적합] 백준 2167번 : 2차원 배열의 합 - Java (0) | 2025.03.30 |
| 백준 7785번 : 회사에 있는 사람 - Java (0) | 2025.03.28 |
| [정렬] 1427번 : 소트인사이드 - Java (0) | 2025.01.21 |

@킴준현 :: 차근차근 꾸준히
포스팅이 좋았다면 "좋아요❤️" 또는 "구독👍🏻" 해주세요!

![[누적합] 백준 2167번 : 2차원 배열의 합 - Java](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FQV7bM%2FbtsM1qkaYmK%2FouqNCPsDsSvrQPiTvJNpG0%2Fimg.png)

![[정렬] 1427번 : 소트인사이드 - Java](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FbboUu2%2FbtsLTqMwv6Y%2FndZwfUnxHeLwLykwYcBCu0%2Fimg.png)